Desibelit keksittiin aikoinaan amerikkalaisessa Bell-puhelinyhtiössä ja niitä käytettiin ilmaisemaan signaalin heikkenemistä puhelinlangoissa. Pian todettiin, että tuli keksittyä vähän liian suuri yksikkö, joten käytännössä puhuttiin desiBelleistä eli kymmenesosista. Toinen L-kirjainkin jäi pois, joten jäljelle jäi desibeli.
Logaritmisuus
Desibeli on logaritminen yksikkö, joka ei kerro lainkaan mitä ollaan mittaamassa. Se kertoo vain kahden arvon suhteesta. Suhde on jakolasku ja siksi alkuperäinen yksikkö supistuu pois. WLAN-maailmassa signaaleja ja lähetystehoja verrataan milliwattiin, jolloin käytetään yksikkönä dBm. Antenneja verrataan yleisimmin isotrooppiseen säteilijään, jolloin yksikkönä on dBi.
Kahta desibeliarvoa verrattaessa yksiköksi jää aina pelkkä dB. Esimerkiksi kohinasuhde on signaali(dBm) miinus taustakohina(dBm) ja sen yksikkö on dB. Esimerkiksi -66dBm-(-96dBm)=30dB. Kyseessä on kohinasuhde, sillä logaritmisella asteikolla vähennyslasku vastaa lineaarisen puolen jakolaskua.
Nollaa ei logaritmisella asteikolla voi esittää. 0dB tarkoittaa yhtäsuuruutta. Esimerkiksi yhden milliwatin teho on 0dBm. Vastaavasti negatiiviset luvut ovat pienempiä kuin vertailukohta. -20dBm on 0,01mW eli milliwatin sadasosa. -70dBm on aika yleinen signaalinvahvuus, joka olisi milliwateissa 0,0000001mW. Logaritminen desibeli tekee siis hyvin pienten ja toisaalta hyvin suurten lukujen esittämisestä ja vertailemisesta helpompaa.
Laskutoimitukset
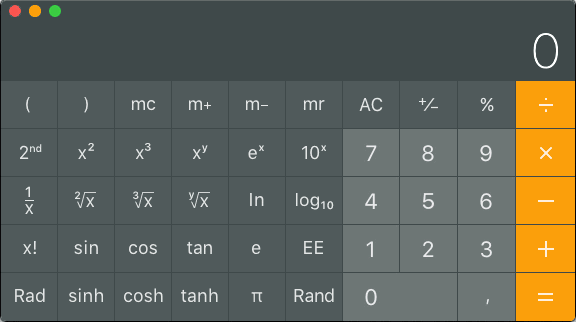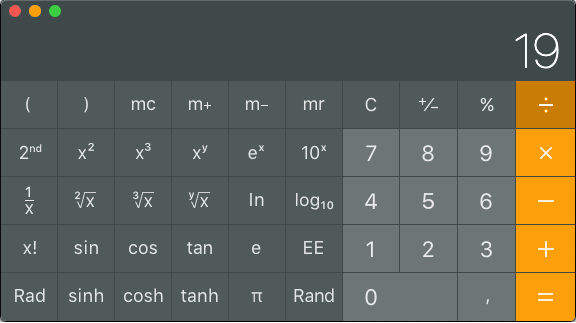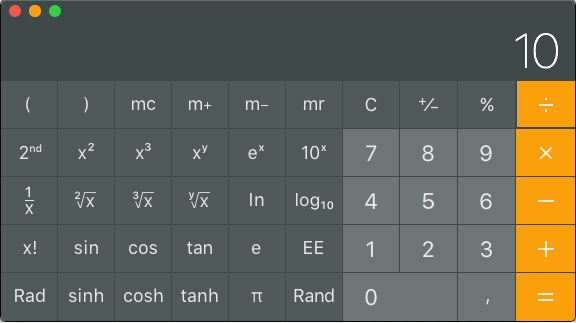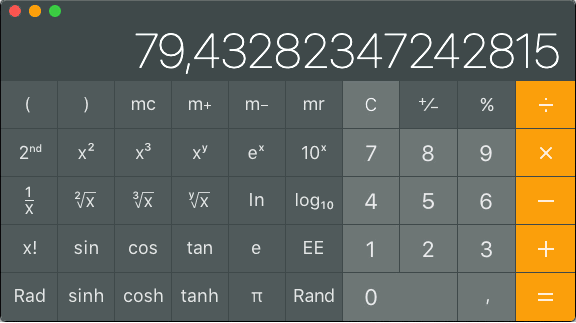
Logaritmeilla kertolaskua vastaa yhteenlasku ja vastaavasti jakolaskua vähennyslasku. Tämä tekee monista laskutoimituksista paljon helpompia. Esimerkiksi halutaan laskea todellinen lähetysteho järjestelmässä, jossa lähettimen teho on 20dBm, antennin vahvistus 15dBi, liittimien hävikki 2dB ja nelimetrisen antennijohdon 3dB per metri:
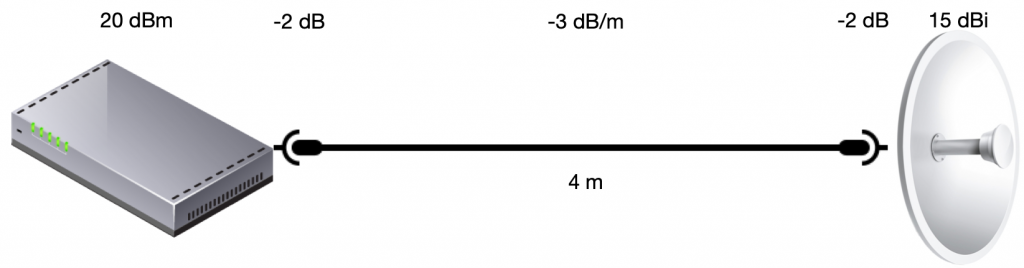
Vastaus on 20-2-4×3-2+15=19dBm
Muunnokset milliwateista desibeleihin ja takaisin voi laskea myös päässälaskuna. Ensin pitää katsoa milliwattien suuruusluokka. Jos se on kymmenissä niin desibeleissä se on 10, sadat on 20 ja tuhannet on 30. Vastaavasti kymmenykset ovat -10, sadasosat ovat -20 ja tuhannesosat ovat -30. Milliwattien kaksinkertaistuminen tarkoittaa kolmen desibelin lisäystä. Esimerkiksi 200mW on luokaltaan satoja eli 20. Sata pitää kertoa kahdella, eli lisätään 3. Vastaus on 23dBm. Vastaavasti 400mW on 20+3+3 eli 26dBm tai 80mW on 10+3+3+3 eli 19dBm.
Desibelit voi muuntaa milliwateiksi samalla tavalla. Jaetaan desibeliarvo kymmenellä (desi-) ja siirretään milliwattien pilkkua yhtä monta askelta. Positiivisella arvolla oikealle ja negatiivisella arvolla vasemmalle. Sitten katsotaan jakojäännöstä ja jokaista kolmosta kohti pitää kertoa tai jakaa kahdella riippuen taas etumerkistä. Esimerkiksi 16dBm on 10mW×2×2 eli 40mW tai -66dBm on 0,000001mW÷2÷2 eli 0,00000025mW.
Laskimella saadaan tietysti tarkka tulos. Montako dBm:ää on 200mW?
Näppäillään 200 log10 × 10 =
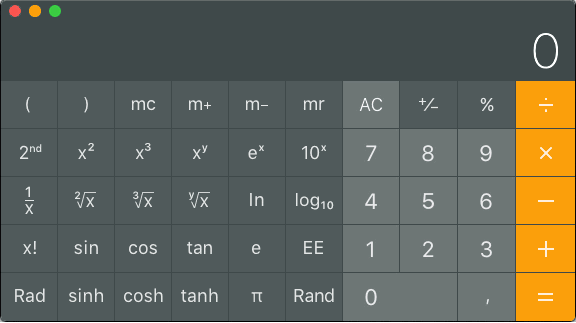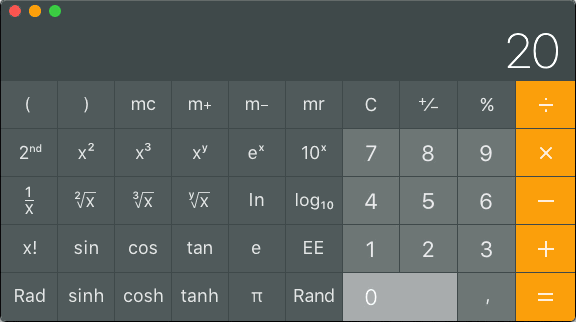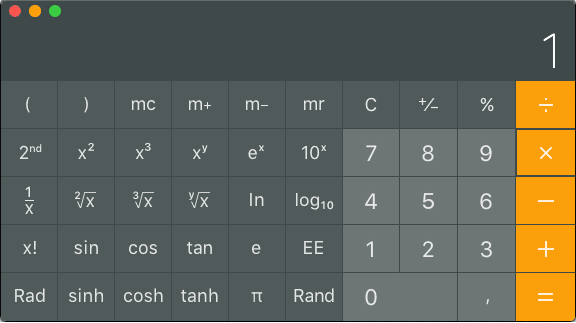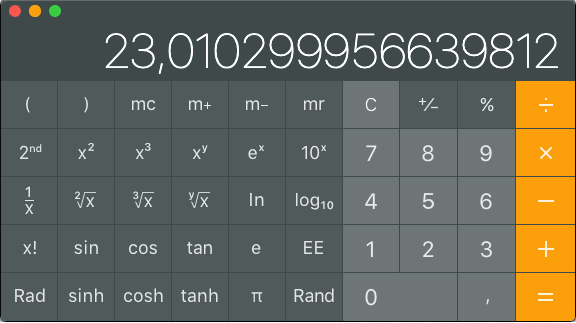
Montako mW:a on 19dBm?
Näppäillään 19 ÷ 10 = 10x