Decibels were invented in the Bell phone company to quantify signal loss in telephone wires. Soon the new unit was discovered to be too large so in practice the tenth of the unit was used, thus deciBells. The second L was dropped so we are using decibels. The original capitalization still shows in the abbreviation dB.
Logarithmicity
Decibel is a logarithmic unit of level that doesn’t contain any actual unit. It is the ratio of two values. Ratio is division so the units cancel out. In Wi-Fi the signal levels and transmit powers are compared to milliwatts so the unit is called dBm. Antennas are most often compared to a isotropic radiator and then the unit is dBi.
If you compare two decibel values to each other, the resulting is always plain dB. For example signal to noise ratio (SNR) is the signal (in dBm) minus the noise level (in dBm) resulting in plain dB. For example -66dBm-(-96dBm)=30dB. It is still a ratio since in the logarithmic scale the subtraction equals division in the linear world.
Zero cannot be represented in a logarithmic scale. 0dB represents equality. For example one milliwatt of power is 0dBm. Respectively negative numbers are smaller than the reference. -20dBm is 0,01mW or a hundredth of a milliwatt. -70dBm is a common signal level, which would be 0,0000001 in milliwatts. Logarithmic decibel makes it easier to present and compare very small and also very large numbers.
Arithmetics
Multiplication turns into addition in logarithmic world and respectively division turns into subtraction. This simplifies many calculations. For example we need to calculate the net transmit level (Effective Isotropic Radiated Power a.k.a. EIRP) for a system where the amplifier outputs 20dBm. The antenna gain is 15dBi, the 4 meter cable loss is 3db per meter and the connector loss is 2dB each:
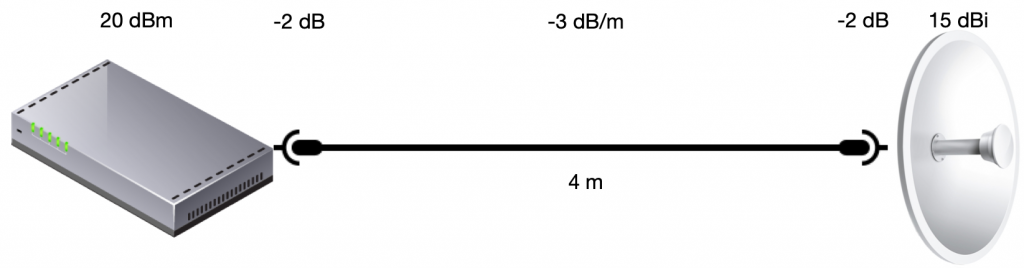
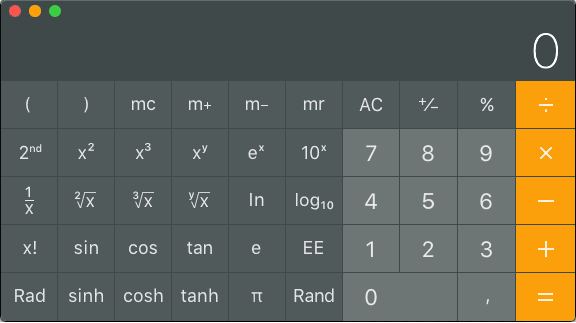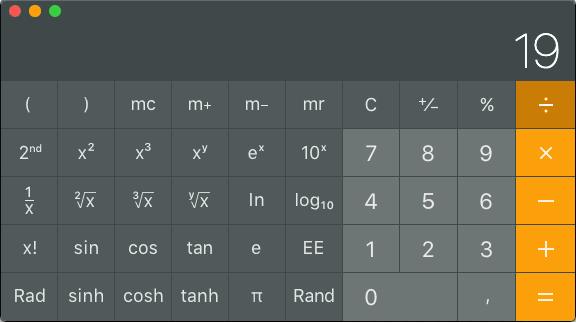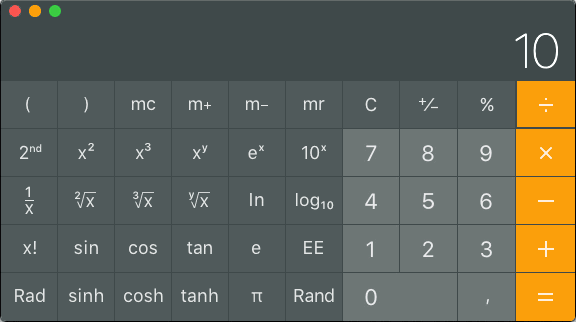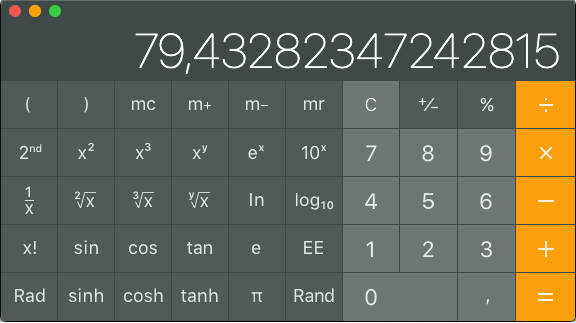
The result is 20-2-4×3-2+15=19dBm
You can convert milliwatts to decibels and back as mental calculations. Let’s start with milliwatts to decibels. Dozens of milliwatts is 10 in dBm, hundreds is 20 and thousands is 30. Respectively tenths is -10, hundredths is -20 and thousandths is -30. Doubling milliwatts equals three decibel increase. For example 200mW is in the hundreds or “20”. One hundred has to be doubled so add 3. The answer is 23dBm. Respectively 400mW is 20+3+3 or 26dBm or 80mW is 10+3+3+3 or 19dBm.
You can convert decibels to milliwatts in the same fashion. Divide the decibel value by ten (to get full Bells). Then move the decimal point by the result. Positive values move the decimal point to the right and negative to the left. Then look at the remainder and multiply (or divide if negative) by two for every three in the remainder. For example 16dBm is 10mW×2×2 or 40mW and -66dBm is 0,000001mW÷2÷2 or 0,00000025mW.
With a scientific calculator you get more exact results, of course. How many dBm is 200mW? Type 200 log10 × 10 =
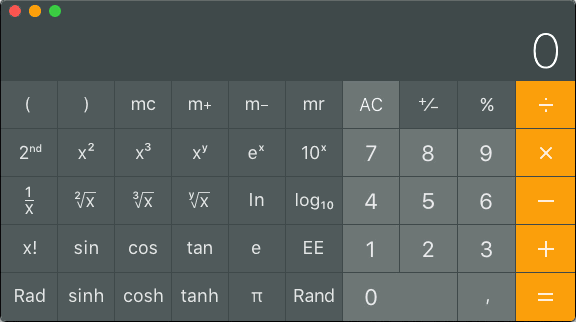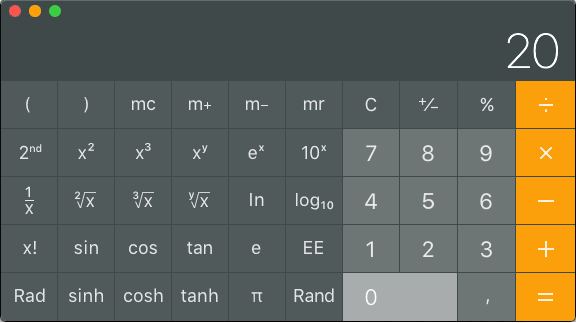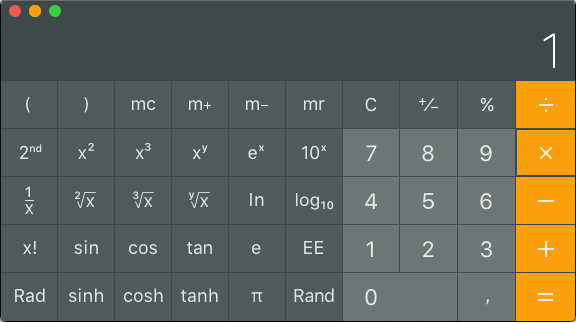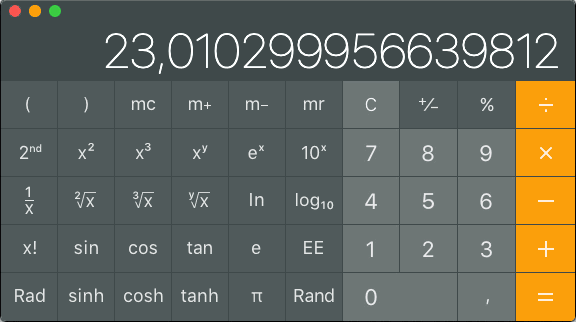
How many milliwatts is 19dBm?
Type 19 ÷ 10 = 10x